The Freeze-Tag Problem
Tools and scripts related to solving and visualizing the Freeze-Tag Problem (FTP).
GitHub Project: sahroush/Geometric-Freeze-Tag-Problem
Authors: Soroush Sahraei et al.
Paper: Geometric Freeze-Tag Problem (arXiv:2412.19706)
Introduction
The Freeze-Tag Problem (FTP), introduced by Arkin et al. in 2002, involves activating a swarm of robots starting from a single active robot, with the goal of minimizing the time to wake up the last robot (the makespan). Our work extends this problem to higher dimensions and refines bounds under different geometric norms. This blog explores how custom visualizers, simulators, and advanced data structures enabled breakthroughs in our research.
Key Contributions from the Paper
- Improved Bounds in 2D and 3D:
- For the Euclidean norm ($\ell_2$) in $\mathbb{R}^2$, we reduced the makespan upper bound from $7.07r$ to $5.064r$.
- In $\mathbb{R}^3$, we established the first bounds: $13r$ for $\ell_1$ and $22.52r$ for $\ell_2$.
- Demonstrated that uniform robot distributions on boundaries do not always yield worst-case makespans in $\ell_2$.
- Practical Configurations:
Explored scenarios where robots lie on 3D boundaries, offering insights for real-world applications like drone swarms and communication.
Tools Behind the Results
1. Visualizers
Visualization tools were critical for:
- Algorithm Validation: Testing wake-up strategies (e.g., linear-time schedules) against known benchmarks like Bonichon et al.’s $7.07r$ bound.
- Counterexample Discovery: Identifying non-optimal configurations where uniform robot distributions fail to maximize makespan.
- 3D Geometry Analysis: Mapping robot trajectories in $\mathbb{R}^3$ under $\ell_1$ and $\ell_2$ norms, revealing path inefficiencies in early strategies.
Example: A simulator snapshot showing robot paths in $\mathbb{R}^3$ under $\ell_1$:
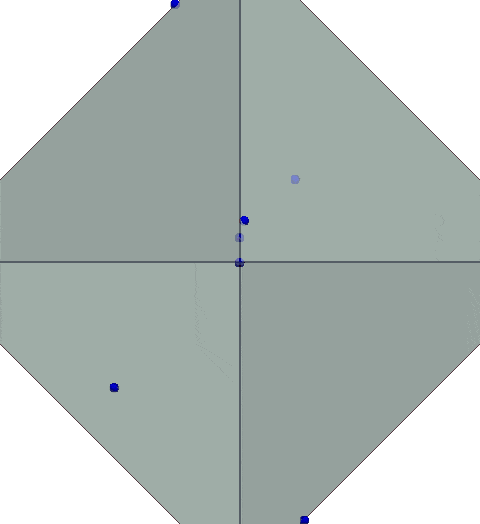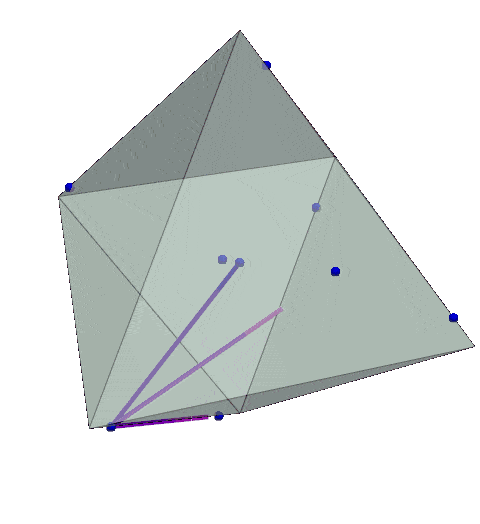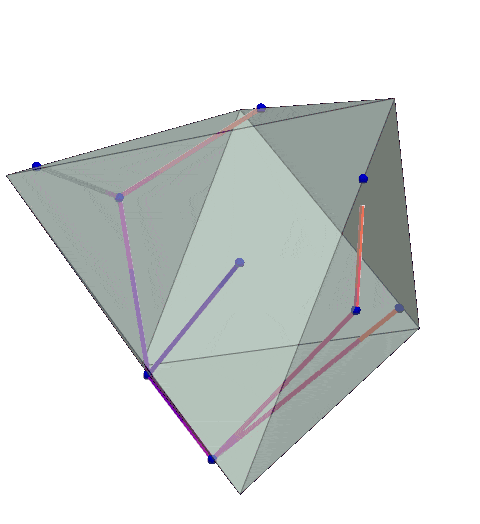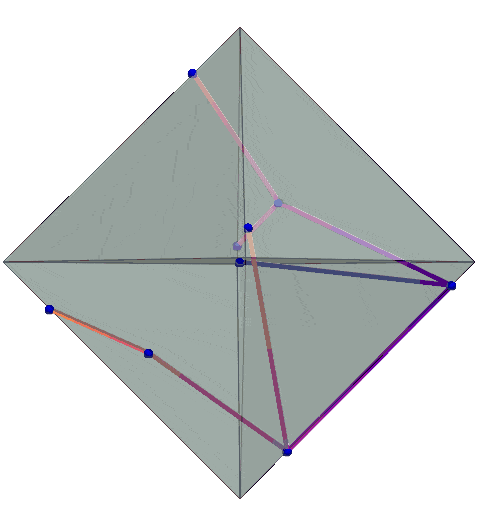
2. Simulators
Our custom simulator enabled:
- Scalability Testing: Handling large $n$ (up to 10,000 robots) to verify linear-time complexity claims.
- Norm-Specific Analysis: Comparing $\ell_1$ and $\ell_2$ performance, e.g., translating $\ell_1$ bounds to $\ell_2$ via scaling factors.
- Boundary Configurations: Simulating robots on spherical/planar surfaces to derive practical wake-up sequences.